MegatronLM: Training Billion+ Parameter Language Models Using GPU Model Parallelism
Published:
Larger language models are dramatically more useful for NLP tasks such as article completion, question answering, and dialog systems. Training the largest neural language model has recently been the best way to advance the state of the art in NLP applications. Two recent papers, BERT and GPT-2, demonstrate the benefits of large scale language modeling. Both papers leverage advances in compute and available text corpora to significantly surpass state of the art performance in natural language understanding, modeling, and generation. Training these models requires hundreds of exaflops of compute and clever memory management to trade recomputation for a reduced memory footprint. However, for very large models beyond a billion parameters, the memory on a single GPU is not enough to fit the model along with the parameters needed for training, requiring model parallelism to split the parameters across multiple GPUs. Several approaches to model parallelism exist, but they are difficult to use, either because they rely on custom compilers, or because they scale poorly or require changes to the optimizer.
In this work, we implement a simple and efficient model parallel approach by making only a few targeted modifications to existing PyTorch transformer implementations. Our code is written in native Python, leverages mixed precision training, and utilizes the NCCL library for communication between GPUs. We showcase this approach by training an 8.3 billion parameter transformer language model with 8-way model parallelism and 64-way data parallelism on 512 GPUs, making it the largest transformer based language model ever trained at 24x the size of BERT and 5.6x the size of GPT-2. We have published the code that implements this approach at our GitHub repository.
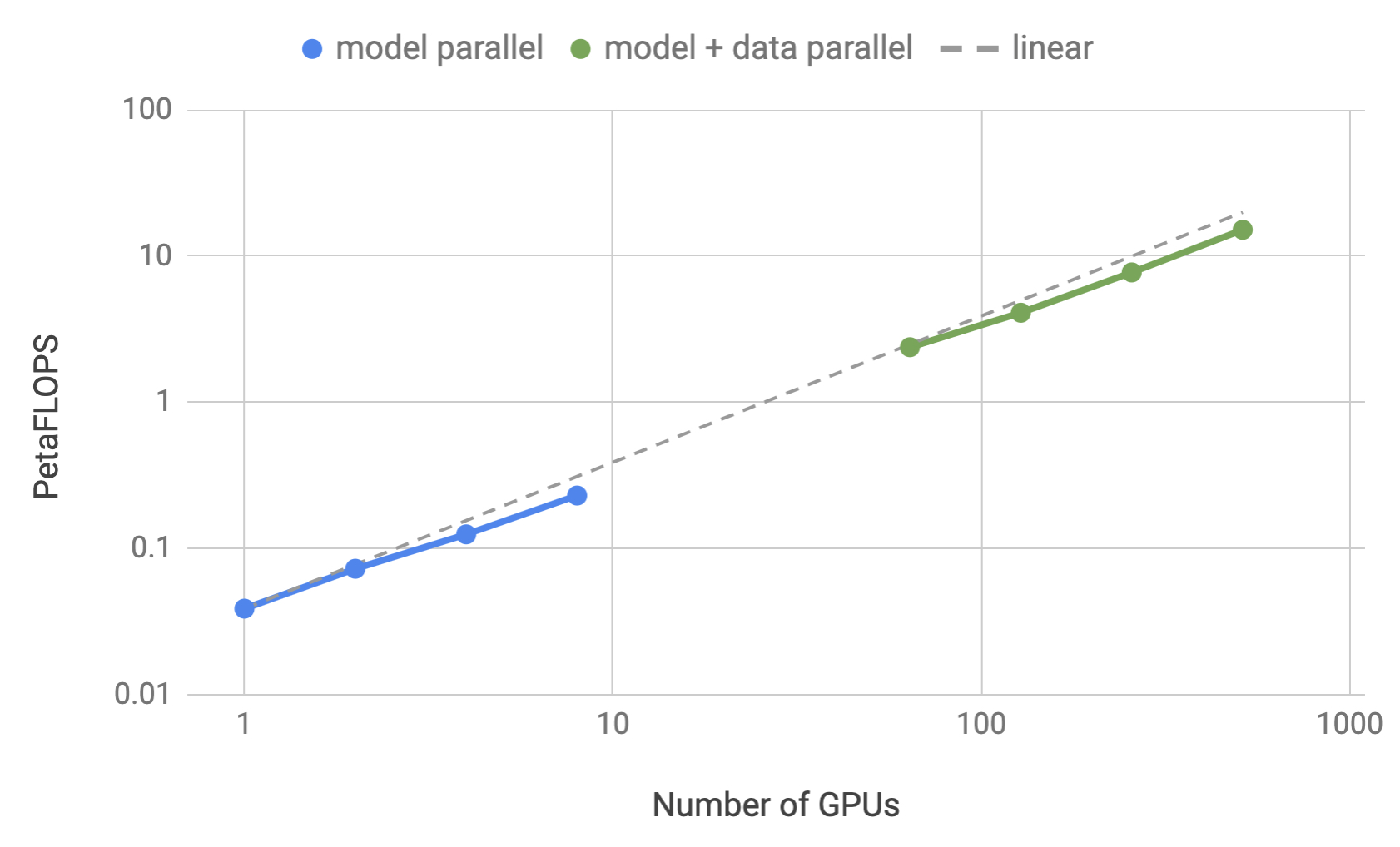
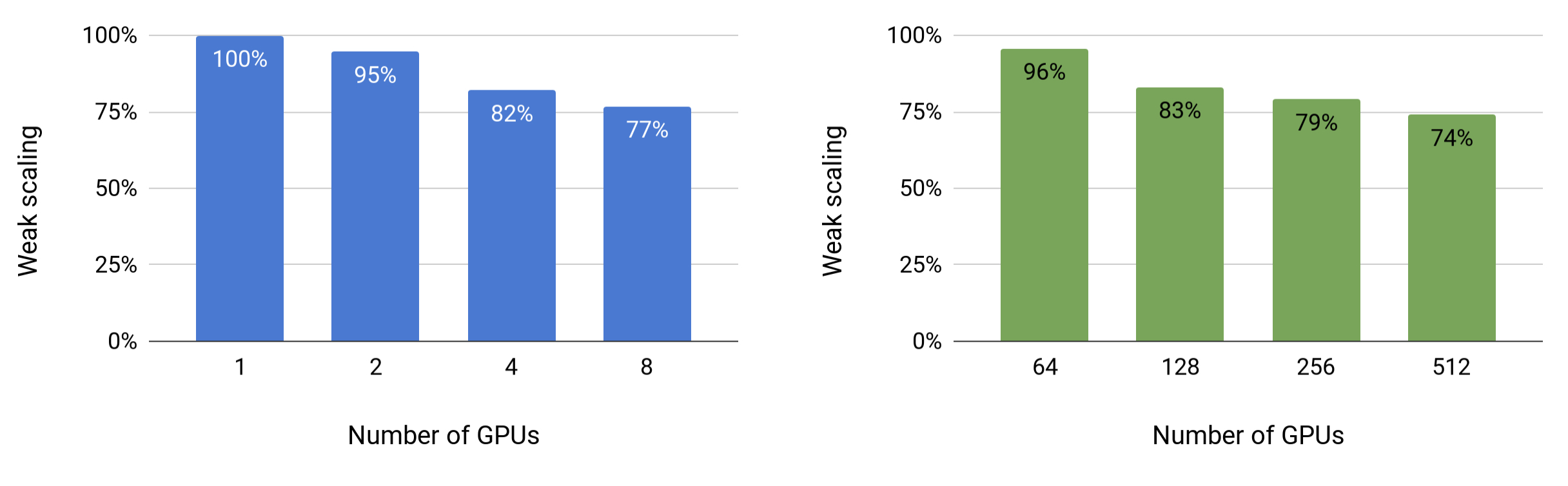
Our experiments are conducted on NVIDIA’s DGX SuperPOD. Without model parallelism, we can fit a baseline model of 1.2B parameters on a single V100 32GB GPU, and sustain 39 TeraFLOPS during the overall training process, which is 30% of the theoretical peak FLOPS for a single GPU in a DGX2-H server. Scaling the model to 8.3 billion parameters on 512 GPUs with 8-way model parallelism, we achieved up to 15.1 PetaFLOPS sustained performance over the entire application and reached 76% scaling efficiency compared to the single GPU case. Figure 1 shows more detailed scaling results.
Multi-GPU Parallelism
The typical paradigm for training models has made use of weak scaling approaches and distributed data parallelism to scale training batch size with number of GPUs. This approach allows the model to train on larger datasets, but has the constraint that all parameters must fit on a single GPU. Model parallel training can overcome this limitation by partitioning the model across multiple GPUs. Several general purpose model parallel frameworks such as GPipe and Mesh-TensorFlow have been proposed recently. gPipe divides groups of layers across different processors while Mesh-TensorFlow employs intra-layer model parallelism. Our approach is conceptually similar to Mesh-TensorFlow, we focus on intra-layer parallelism and fuse GEMMs to reduce synchronization. However, we only make a few targeted modifications to existing PyTorch transformer implementations to employ model parallelism for training large transformers. Our approach is simple, does not require any new compiler or code re-wiring for model parallelism, and can be fully implemented with insertion of few simple primitives (f and g operators in Figure 2) as described in the remainder of this section.
We take advantage of the structure of transformer networks to create a simple model parallel implementation by adding a few synchronization primitives. A transformer layer consists of a self attention block followed by a two-layer multi-layer perceptron (MLP). We introduce model parallelism in both of these blocks separately. We start by detailing the MLP block as shown in Figure 2a. This block consists of two GEMMs with a GeLU nonlinearity in between followed by a dropout layer. We partition the first GEMM in a column parallel fashion. This allows the GeLU nonlinearity to be independently applied to the output of each partitioned GEMM. The second GEMM in the block is parallelized along its rows and takes the output of the GeLU layer directly without requiring any communication. The output of the second GEMM is then reduced across the GPUs before passing the output to the dropout layer. This approach splits both GEMMs in the MLP block across GPUs and requires only a single all-reduce operation in the forward pass (g operator) and a single all-reduce in the backward pass (f operator).
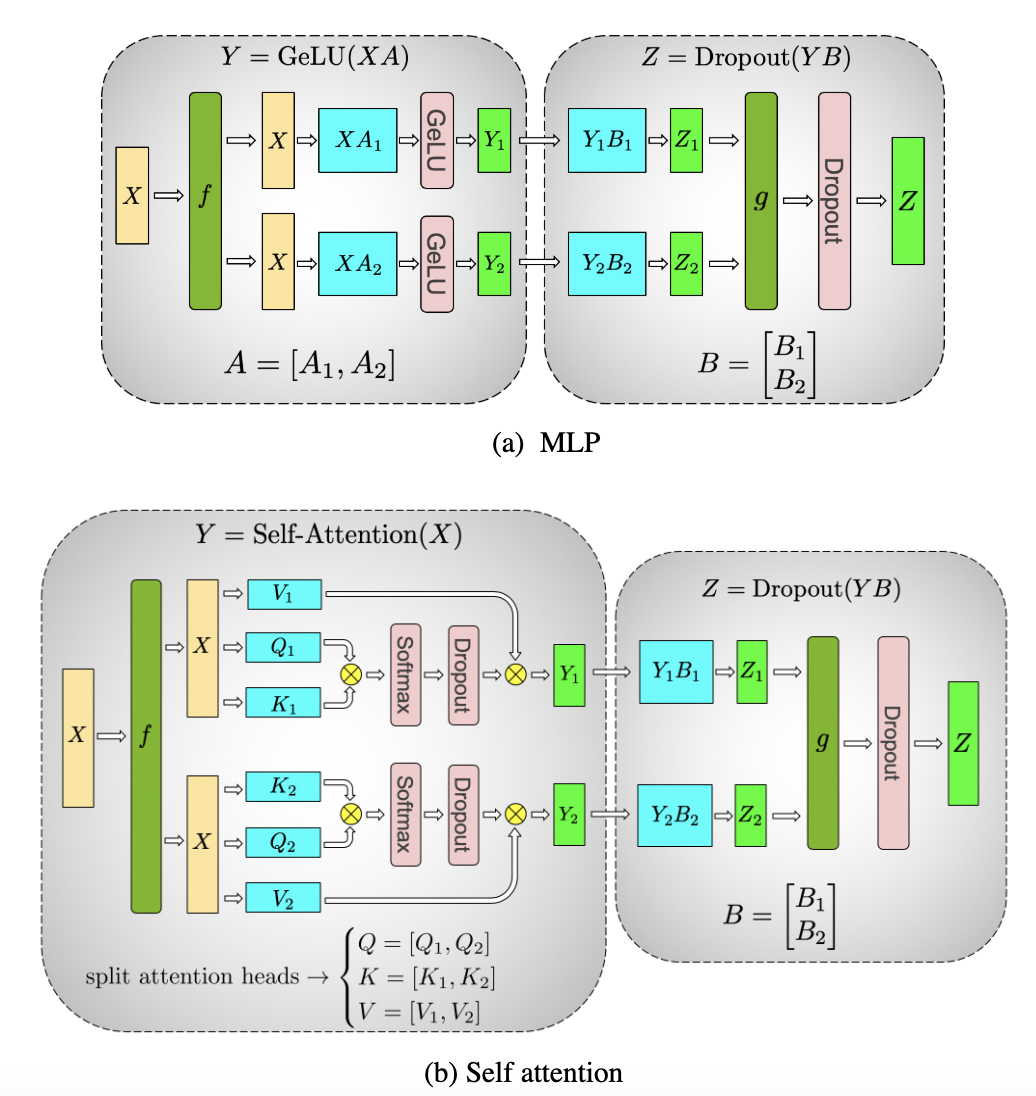
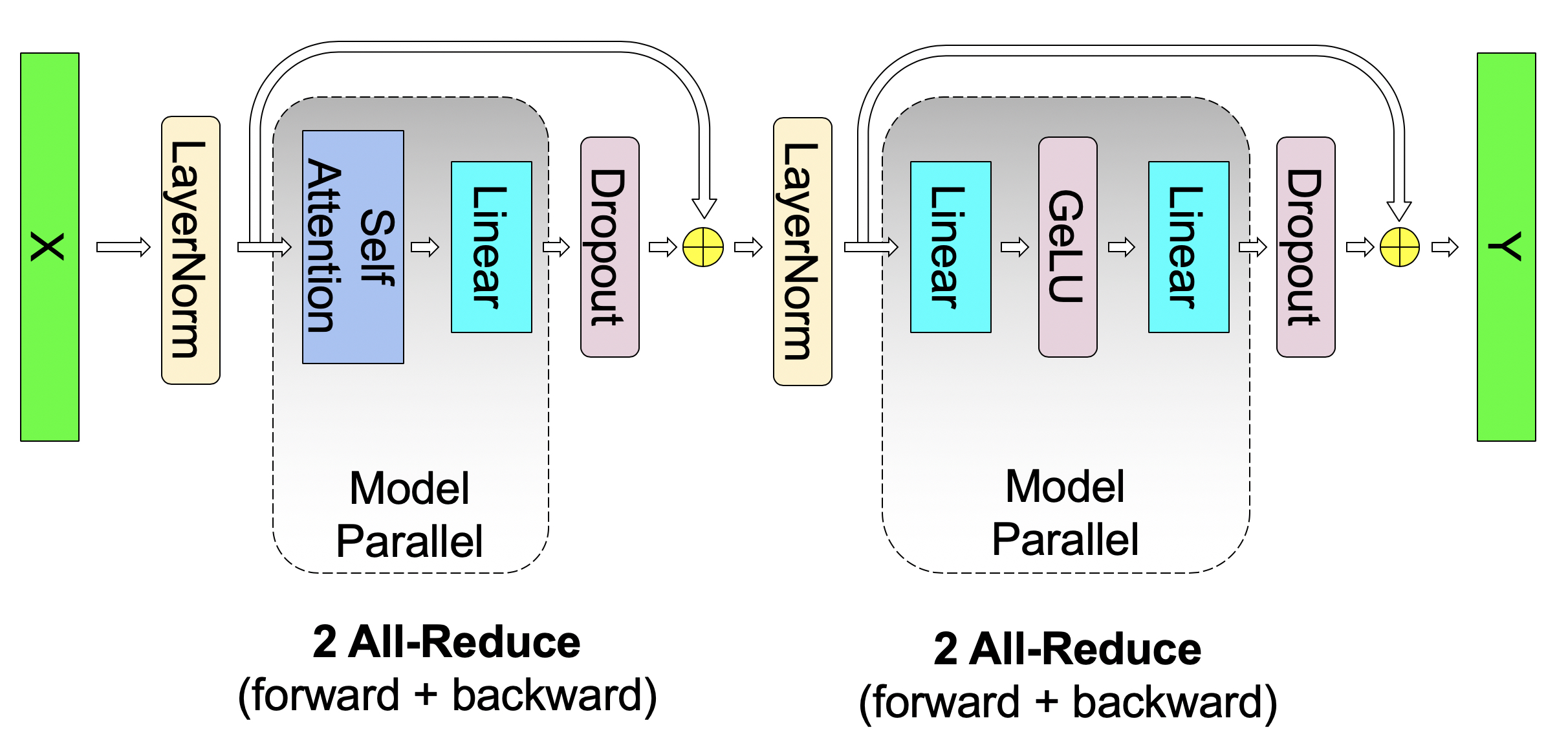
As shown in Figure 2b, for the self attention block, we exploit inherent parallelism in the multihead attention operation, partitioning the GEMMs associated with key (K), query (Q), and value (V) in a column parallel fashion such that the matrix multiply corresponding to one attention head is done locally on one GPU. This allows us to split per attention head parameters and workload across the GPUs, and doesn’t require any immediate communication to complete the self-attention. The subsequent GEMM from the output linear layer (after self attention) is parallelized along its rows and takes the output of the parallel attention layer directly, without requiring communication between the GPUs. This approach for both the MLP and self attention layer fuses groups of two GEMMS, eliminates a synchronization point in between, and results in better scaling performance. This enables us to perform all GEMMs in a simple transformer layer using only two all reduces in the forward path and two in the backward path (see Figure 3). Lastly, the output logit layer is also partitioned along the vocabulary dimension, and to avoid a massive all-gather across the vocabulary dimension, we fuse this layer with the cross entropy loss.
This approach is simple to implement, because it requires only a few extra all-reduce operations be added to the forward and backward pass. It doesn’t require a compiler, and is orthogonal to the kind of pipeline model parallelism advocated by approaches such as gPipe.
Performance
To test the computational performance of our implementation, we consider GPT-2 models with four sets of parameters detailed in Table 1. To have consistent GEMM sizes in the self attention layer, the hidden size per attention head is kept constant at 96 while the number of heads and layers are varied to obtain configurations ranging from 1 billion to 8 billion parameters. The configuration with 1 billion parameters fits on a single GPU whereas the 8 billion parameter models requires 8-way model parallelism (8 GPUs). The original vocabulary size was 50,257, however, to have efficient GEMMs for the logit layer, it is critical for the vocabulary size to be a multiple of 128 as well as the number of model parallel GPUs. Since we study up to 8-way model parallelism, we pad the vocabulary such that it is divisible by 128x8=1024, resulting in a padded vocabulary size of 51,200. We study both model and model+data parallel scalings. For the model parallel scaling, a fixed batch size of 8 is used across all configurations. Data parallel scaling is necessary for training many state of the art models which typically use a much larger global batch size. To this end, for the model+data parallel cases we fix the global batch size to 512 for all experiments which corresponds to 64-way data parallelism.
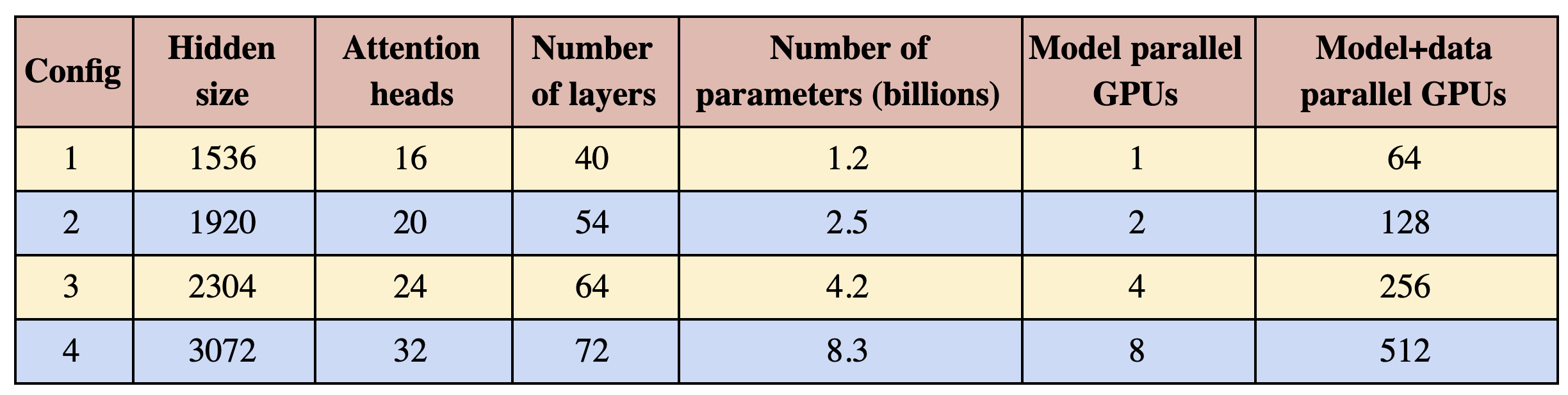
All of our experiments are conducted on NVIDIA’s DGX SuperPOD and we use up to 32 DGX-2H servers (a total of 512 Tesla V100 SXM3 32GB GPUs). This system is optimized for multi-node deep learning applications, with 300 GB/sec bandwidth between GPUs inside a server and 100 GB/sec of interconnect bandwidth between servers. Throughout this section, we will showcase weak scaling with respect to the model parameters for both model parallel and model+data parallel cases. Weak scaling is typically done with scaling the batch-size, however, this approach does not address training large models that do not fit on a single GPU and also convergence performance degrades for large batch sizes. In contrast, here we use weak scaling to train larger and larger models that were not possible otherwise. The baseline for all the scaling numbers is the first configuration in Table 1 running on a single GPU.
Figure 4 shows scaling values for both model and model+data parallelism. We observe excellent scaling numbers in both settings. For example, the 8.3 billion parameters case with 8-way (8 GPU) model parallel achieves 77% of linear scaling. Model+data parallelism requires further communication of gradients after the back-propagation step and as a result the scaling numbers drop slightly. However, even for the largest configuration (8.3 billion parameters) running on 512 GPUs, we still achieve 74% scaling relative to the strong baseline single gpu configuration (1.2 billion parameters).
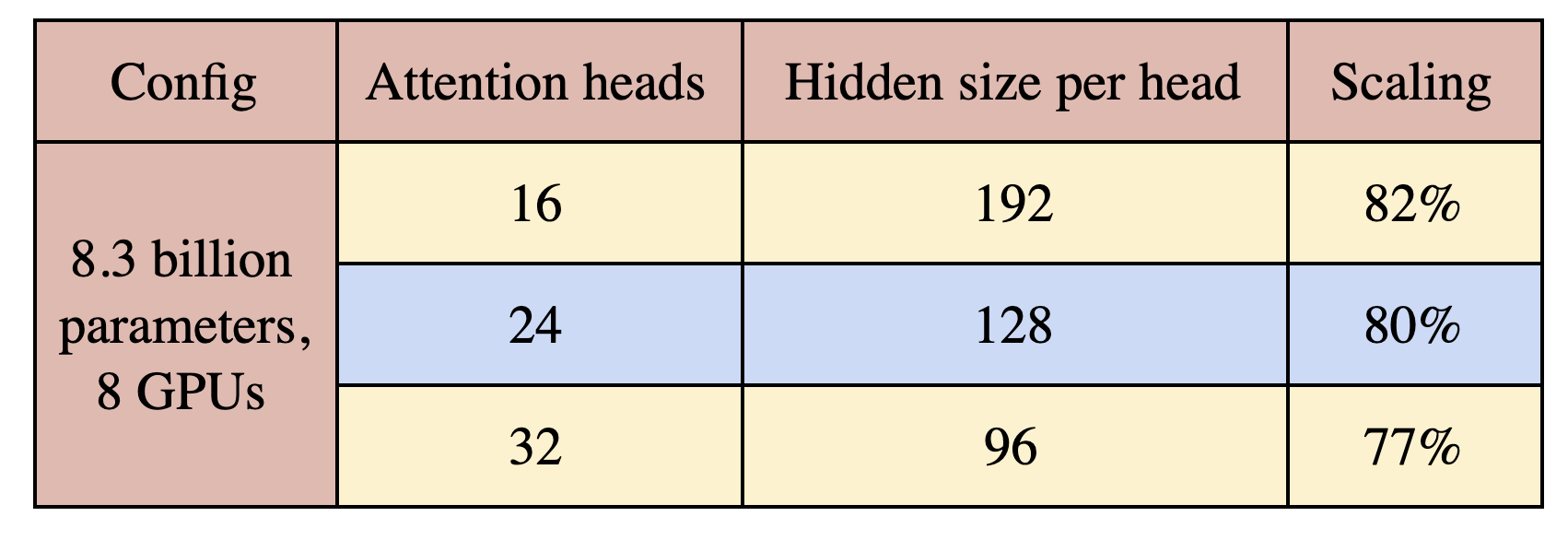
Finally, we study the effect of attention heads on model parallel scaling. To this end, we consider the 8.3 billion parameter configuration with 8-way model parallelism and vary the number of heads from 16 to 32. The results are presented in Table 2. As the number of attention heads increases, some of the GEMMS inside the self-attention layer become smaller and also the number of elements in the self attention softmax increases. This results in a slight decrease in scaling. Future research should be wary of this hyperparameter to design large transformer models that balance model performance and model efficiency.
GPT-2 Training
To train our GPT-2 model we created an aggregate 174GB dataset (~4.5x larger than WebText) consisting of Wikipedia, OpenWebText, RealNews, and CC-Stories. We performed additional filtering to remove malformed, short or duplicate documents less than 128 tokens. To clean the datasets we used the ftfy library and then removed non-english content using the langdetect library. We further cleaned our dataset by removing WikiText test-set content and remove duplicates by using LSH filtering with a jaccard index of 0.7. The dataset ended up with approximately 40 million documents. For training, we randomly split the WebText dataset into a 29:1 ratio to obtain training and validation sets, respectively.
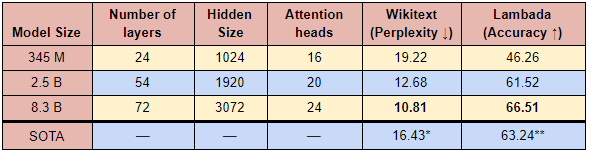
We consider training 3 model sizes: 355 million, 2.5 billion, and 8.3 billion. The 355 million parameter model is similar to the one used in GPT-2, and uses 16 attention heads. The 2.5 billion and 8.3 billion parameters models are detailed in Table 1, except that for the 8.3 billion parameter case, we use 24 attention heads. Learning rates in all cases are set to $1.5\times 10^{-4}$ with single cycle cosine annealing and 3000 iteration warmup. We clamp our learning rate to a minimum value of $1\times 10^{-5}$. A gaussian distribution with zero mean and standard deviation of 0.02 is used for weight initialization and we scale the weights of layers preceding residual connections by $\frac{1}{\sqrt{2N}}$ where $N$ is the number of layers. In all cases, a dropout of 0.1 is used.
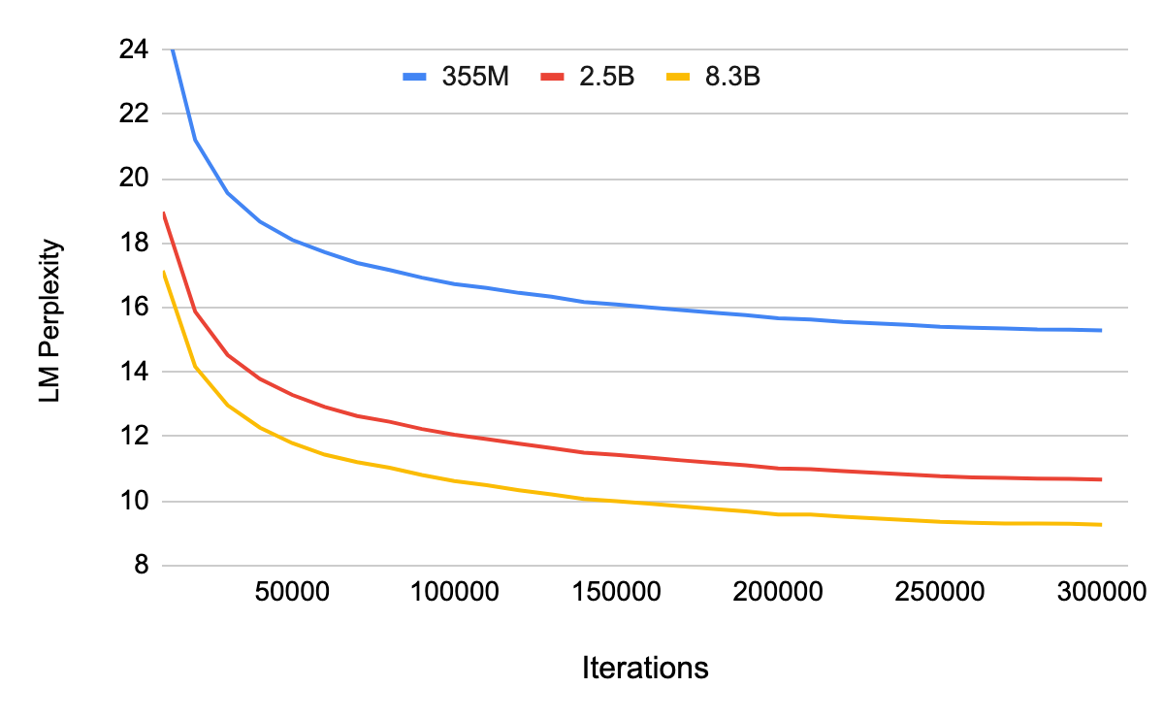
Figure 5 shows validation perplexity as a function of number of training iterations for different model sizes. At validation time we find empirically that larger models lead to lower validation perplexities (Figure 5). Our 8.3B model achievs a validation perplexity of 9.27. An epoch is defined as 68,507 iterations to train over the entire 174GB corpus.
GPT-2 Evaluation
To analyze the performance of training large language models, we compute perplexity on the WikiText-103 dataset and cloze-style prediction accuracy on the LAMBADA dataset. Earlier we made sure to remove WikiText test set content to avoid leakage. Our resulting dataset has a WikiText 8-gram overlap of 10% which is similar to the 9% 8-gram overlap between the WikiText-103 train and test sets. As expected, the WikiText perplexity decreases and LAMBADA accuracy increases with the growth of the model size (Table 3). At a respective WikiText perplexity of 12.68 and 10.81 both our 2.5B and 8.3B models surpass the previous state of the art perplexity of 16.43 set by Krause et. al. Our models achieve 61.52% and 66.51% accuracy on LAMBADA even without any stopword filtration, surpassing Radford et. al. We describe our evaluation methodologies below; however, more details are available in our github repository.
Conclusion
In this work, we built the world's largest transformer based language model on top of existing deep learning hardware, software, and models. In doing so, we successfully surpassed the limitations posed by traditional single GPU training by implementing a simple and efficient model parallel approach with only a few targeted modifications to the existing PyTorch transformer implementations. We efficiently train an 8.3 billion parameter language model (24x and 5.6x larger than the size of BERT and GPT-2, respectively) on 512 NVIDIA V100 GPUs with 8-way model parallelism and achieve up to 15.1 PetaFLOPS sustained over the entire application. With weak scaling, we found that increasingly large transformer models can be trained in a similar amount of time compared to their smaller counterparts and can demonstrably improve performance. Our 8.3B model exemplifies this by setting new state of the art results for both WikiText-103 (10.81 perplexity) and LAMBADA (66.51% accuracy). We open source our work so that the community may reproduce our efforts and extend them.
Update 9/5/2019: Larger dataset and stricter lambada formulation
Appendix
WikiText Perplexity:
Perplexity is the exponentiation of the average cross entropy of a corpus. This makes it a natural evaluation metric for language models which represent a probability distribution over entire sentences or texts. We make note of the detailed methods we use to compute perplexity for the sake of reproducibility. $$ PPL= \exp\left(-\frac{1}{T_o}\sum_{t}^{T} \text{log}\;P(t\vert 0:t-1)\right)$$ The WikiText-103 test corpus already comes pre-tokenized with word-level tokens that prior work has used to compute perplexity. To evaluate model perplexity fairly and consistently, we normalize by the original number of word-level tokens, $T_o$, rather than the number of subword tokens, $T$, that were present in the tokenized data. Additionally, to alleviate distributional mismatch caused by WikiText processing artifacts, we first preprocess the WikiText-103 test dataset with invertible de-tokenizers to remove various artifacts related to punctuation and whitespace. The value of $T_o$ is calculated before this preprocessing. For WikiText-103's test set we arrive at $T_o=245566$ and $T=270329$. Lastly, to accommodate the transformer’s fixed window input size and inability to attend to all tokens [0, t-1], we utilize a sliding window approach with a size of 1024 tokens, and a stride of 32 tokens to compute perplexity.
Cloze Accuracy:
Cloze-style datasets like LAMBADA are designed to measure a model's ability to operate in and reason about long-term contexts. Handling long term contexts is crucial for state of the art language models to solve problems like long-form generation and document-based question answering. Cloze-style reading comprehension uses a context of word tokens $x=x_{1:t}$ with one token $x_j$ masked; the model's objective is to correctly predict the value $y$ of the missing $j^{\text{th}}$ token based on its understanding of the surrounding context. LAMBADA uses cloze-style reading comprehension to test generative left-to-right language models by constructing examples of 4-5 sentences where the last word in the context $x_t$ is masked. Our models utilize subword units, so for our version of LAMBADA evaluation we utilize the raw, unprocessed LAMBADA dataset, and require that our model predict the multiple $x_t$ subwords that make up the last word token. We use teacher forcing in our predictions, and consider an answer correct only when all output subword predictions are correct. This formulation is equivalent to the original task of word prediction.
